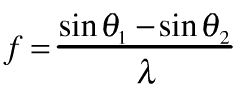
Holographic Imaging |
MAS.450/854
|
Recently in class, we introduced the equation for calculating the local spatial frequency of the interference pattern formed at a point on a two dimensional surface by two rays of light coming from two mutually coherence sources:
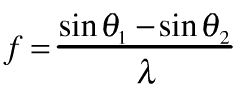
This equation is called sometimes called the interference equation. In the equation, lambda is the wavelength of the light from the two sources (commonly measured in nanometers). The spatial frequency f is measured in cycles per unit length (or, equivalently, line-pairs per unit length). We will most commonly use cycles per millimeter when talking about holographic fringe patterns. The two angles are measured as shown below:
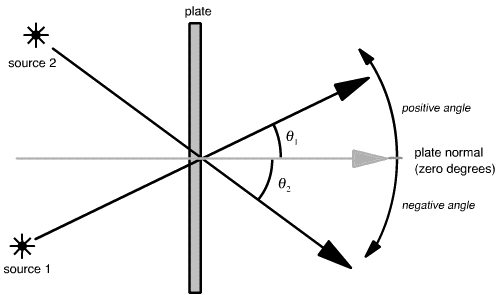
What happens when a spatial frequency is negative? Well, a negative spatial frequency is the essentially the same as a positive spatial frequency; you can in fact consider spatial frequency to be only positive, and the equation above to include an absolute value sign.
Here are a few simple examples of how the interference equation can be used.
Q: Using the above diagram, say that theta1 is 30 degrees and theta2 is -40 degrees, what is the spatial frequency of the resulting fringe pattern, at the point on the plate shown, made with a HeNe laser?
A: Plugging directly into the equation, and adjust the units of wavelength to give us our desired units of cycles/mm:
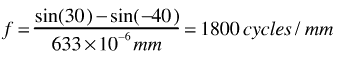
Q: Two sources are located one meter behind a plate (which is axis-aligned as shown above). One source is located 1cm above the "z" axis, the other 1cm below. Find the spatial frequency.
A: In this case, it’s helpful to use the "small angle" approximation, which says that for small angles measured in radians, x is appoximately equal to sin(x) is appoximately equal totan(x). Here, tan(theta) is 0.01, and sin(—theta) = —sin(theta)so we have:
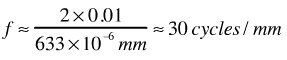
Remember, angles are always measured with respect to the plate normal. If the plate isn’t aligned with an axis, you must do a "change of coordinate system" and convert all angles to a plate-centric coordinate system where the plate normal is 0 degrees.
Using exactly the same mathematics used in the problems shown above, you can determine angles between sources given an interference pattern of a known spatial frequency. Problem set #1 asks you to do just that. Since the fringe pattern is coarse (and easy to measure) when the sources that create it are angularly close together (and probably harder to measure), this technique can be quite useful as a measurement tool.