- the problem -

The problem that I explored was to get an embodied synthetic creature to reliably infer the affective state of another creature from its perception of that creature's body configuration. If all that wolf B can perceive of wolf A is his body pose, then what can wolf B conclude about wolf A's affective state?

- the representation -

This project was developed within the context of the Synthetic Characters Group codebase, building upon the AlphaWolf project in particular. The two elements of our framework that are most imporant for this project are our emotion representation and motor representation.

Emotion representation:
We use a dimensional emotion model, with dominance and arousal axes. For this project, and for the AlphaWolf project in general, the primary focus is on just the dominance axis.

Motor representation:
Our motor representation is based on the idea of verbs and adverbs: what is the creature doing, and in what manner are they doing it? (i.e. sitting sadly, walking drunkenly, etc.)

Each creature has a motor system that consists of a directed graph of poses. At every tick, the creature's joint angles are derived from one such pose in the graph. Behaviors such as galloping or barking can be thought of as trajectories through this pose graph.

There are two different types of poses in the motor graphs used in the wolves: blended poses, and non-blended poses. Non-blended poses simply specify the creature's joint angles exactly. Blended poses each contain a set of example poses. The creature's joint angles are derived by blending among these example poses based on a corresponding set of blend weights. These blend weights are calculated from adverb parameters specified by the creature's behavior system. An example of blended poses are the poses from the growl behavior, which have both dominant and submissive examples. More complicated blends are possible, such as for the gallop behavior, which has 2 (dominant-submissive) x 3 (turn left-straight-turn right) x 2 (adult-pup) = 12 examples per pose.

- approach -

Given this motor representation, the problem we are trying to solve can be broken up into the following three parts, if we make use of the fact that all of our wolves have the same skeletal structure and motor graph structure:

1. Given an image of another creature, infer its joint angles.
2. Given its joint angles, find the pose in the motor graph that (most likely) generated these angles, and if this pose is a blended pose, infer the corresponding blend weights.
3. Given a pose in the motor graph and blend weights if the pose is a blended pose, infer the affective state of the perceived creature.

For this project I focused on the third of these tasks. I spent enough time thinking about the first two problems to verify that they are in fact tractable, though difficult.

The approach that I took was to have each creature learn a mapping from pose data to affect values by storing affect information in its own motor graph. Reliable instances of this mapping are derived from self-observation: on every tick, each creature adds its current affect value to the affect model associated with its current pose in the pose graph. Thus the wolves recognize how each other feels by remembering how they themselves feel when they are in that pose configuration.

To support this type of learning I developed two types of affect model: one for non-blended poses and one for blended poses.

The non-blended pose affect model simply maintains a one-dimensional distribution of affect values, with mean and variance statistics.

The blended pose affect model is more complicated. My approach was to learn an affect value for each of the blend examples. Given a set of blend weights, then, the inferred affect value is calculated by simply blending linearly amongst these learned example values.

In order to learn an affect value for each of the blend examples, we maintain a two-dimensional distribution for each example. The points in each distribution are of the form (blend weight, affect value). The points are prioritized to maintain maximal spacing along the blend weight axis. Below is the distibution for the example gallop-straight-dominant-pup, which is contained within one of the blended poses of the gallop behavior.

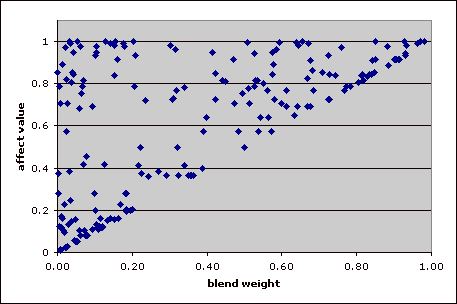
Our job is to discover the affect value associated with a blend weight of 1; i.e. when this blend example is being used exclusively, what is the affect value? My approach to this problem is to try to fit lines to the "top" and "bottom" of the distribution. These lines are then evaluated at 1 to find the affect value. If these lines do not converge nicely or if there is insufficient data, we simply find the line of best fit of the distribution and evaluate it at 1.

- evaluation -

I incorporated the affect recognition system described above into two different versions of the AlphaWolf environment: one interactive, and one non-interactive. In the interactive version, the grey pup could be guided around the world and directed to interact with his littermates by means of a keyboard and mouse. In the non-interactive version, four wolf pups autonomously engaged in dominance and submission behaviors with each other.

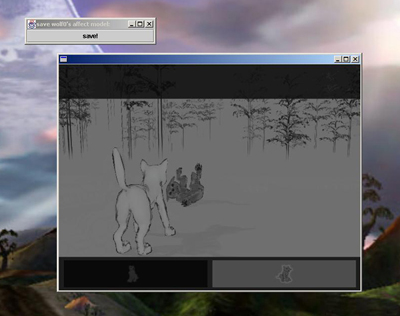
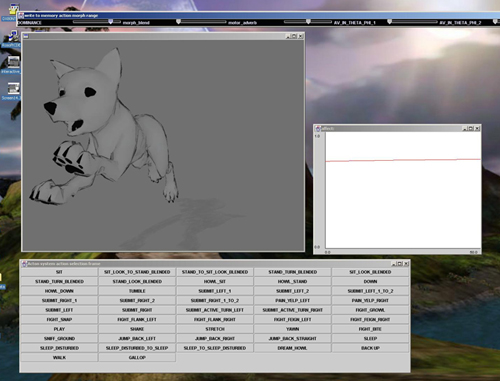
I also developed a test environment so that I could verify the functionality of the system. The state of the grey pup's pose affect models could be saved out of either of the two environments described above and loaded into the test environment. Here I could push buttons to direct the pup through specific trajectories in its motor graph, and could also specify adverb parameters (such as the dominance variable itself) directly. A strip chart tracked the affect value inferred by the recognition system.

Below is a graph derived from a run of the non-interactive environment, showing the error in the pups' perceptions of each other's emotional state over time. The pups become more accurate as time passes. The error will never stabilize at 0, however, since some poses are affect-neutral, and thus the affective state of a pup in such a pose cannot be inferred with perfect accuracy.