Non-parametric Classification of Facial Features

 

 

Hyun Sung Chang

 

Department of Electrical Engineering and Computer Science

Massachusetts Institute of Technology

E-mail: hyunsung@mit.edu

 

 

 

Problem statement

 

In this project, I attempted to classify facial images based on various external characteristics, such as gender, expression, and accessories they are taking on.

Rather than extracting any particular parameters describing faces, e.g., the distances among eyes, nose, and mouse, I used grey-scale face images themselves, fitted to 128x128 window, as the inputs.

 

 

Dataset

 

The dataset used for this project together with detailed description is available here at the course website. The dataset consists of 2,000 training face images (faceR, 1,997 of them labeled) and 2,000 test face images (faceS, 1,996 of them labeled). Because the image size is 128x128, each image can be considered as a data point in a huge dimensional space. The dimensionality reduction has been conducted using principal component analysis (PCA) on 100 sample faces, all from the training dataset, so each image can be represented by 99 eigenface coefficients, as well as the mean face.

 

The composition of dataset is shown in Table 1. For example, notice that, in terms of expression, “funny” faces were significantly fewer than the other two classes and that few people wore glasses or bandana. One interesting thing is that no bandana image was included in the samples used to generate the eigenfaces.

 

 

Table 1. Dataset composition

 

gender

 

 

expression

male

female

 

serious

smiling

funny

Eigenface generating data

61/100

39/100

 

Eigenface generating data

45/100

51/100

4/100

Training data (faceR)

1,150/1,997

847/1,997

 

Training data (faceR)

917/1,997

1,043/1,997

37/1,997

Testing data (faceS)

1,277/1,996

719/1,996

 

Testing data (faceS)

1,097/1,996

836/1,996

63/1,996

 

 

glasses

 

 

bandana

on

off

 

on

off

Eigenface generating data

4/100

96/100

 

Eigenface generating data

0/100

100/100

Training data (faceR)

59/1,997

1,938/1,997

 

Training data (faceR)

13/1,997

1,984/1,997

Testing data (faceS)

8/1,996

1,988/1,996

 

Testing data (faceS)

8/1,996

1,988/1,996

 

 

Objective of this project

 

The objective of this project lies in two aspects:

1)      to practice with meaningful classification problem using the methods learned from the class;

2)      to look into inherent limitations of PCA approach.

 

 

Eigenface representation

 

Let  be eigenfaces and  be the sample faces used to generate the set of eigenfaces. The PCA finds  so that  can be well represented by their linear combinations. Let  be an arbitrary face and  be its eigenface representation, that is, .

Note that  is just a linear combination of , which implies that the sensitivity issue should be aroused. For example, because there was no bandana image in , we may see that  and  may be significantly different from each other if  is a facial image of the person who is wearing a bandana.

The approximation error between  and  can be measured in terms of peak-signal-to-noise-ratio (PSNR) defined by

    ,

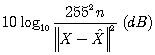where  is the number of pixels.

 

 

Figure 1 shows a bandana image example. The PSNR is as low as 14.47dB. Note that, in eigenface representation, other regions than the bandana pixels were also severely distorted as a result of making best efforts to compensate for the bandana region. This may lead to the classification errors even also for the other criteria, not only for the bandana.

 

        

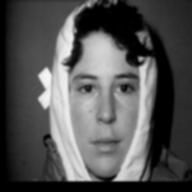
Figure 1. Bandana image example and its eigenface approximation.

 

 

Figure 2 shows the actual PSNR distribution for the training dataset and the test dataset. The images in the test dataset show somewhat low PSNR; for some particular samples, the PSNR was significantly low. This low PSNR may contribute to the classification error.

 

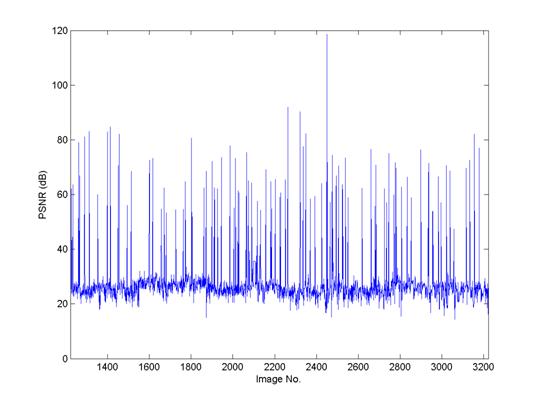
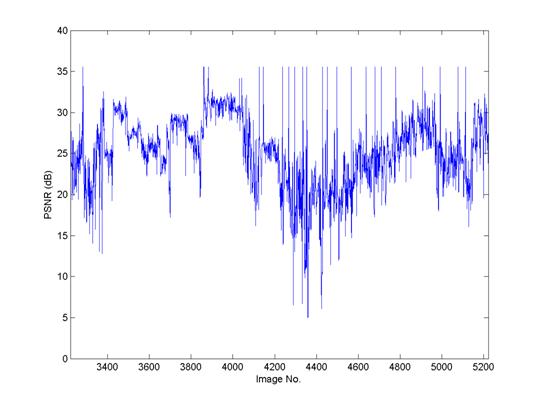
Figure 2. PSNR distribution of each face image in training dataset (faceR) and in test dataset (faceS). (left: faceR, right: faceS)

 

 

Figure 3 illustrates how the discriminant value and the PSNR for gender classification (+ = male, - = female) when a linear discriminant was used. Note that a majority of male samples of high PSNR were correctly classified. For the female samples, such a correlation was not that noticeable; instead, the discriminant value and the PSNR looked rather uncorrelated. I think this may be because of the inherent ill-performance of our classifier against female images (See Table 2)

 

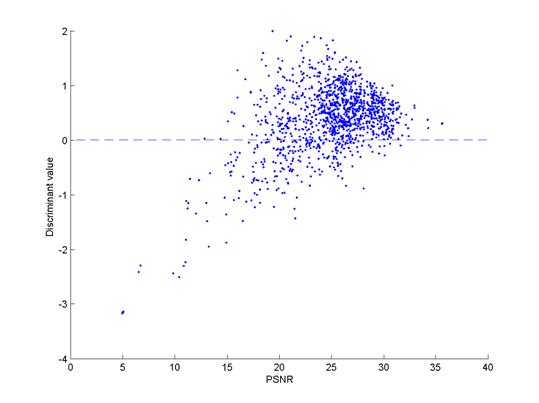
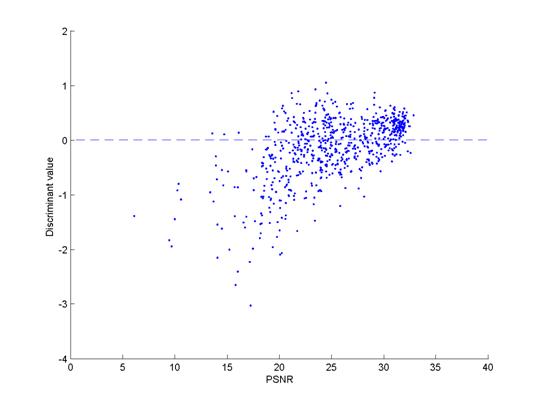
Figure 3. Plot of discriminant value versus PSNR for male and female face samples. (left: male, right: female)

 

 

 

Classification practice

 

For this part of experiment, the following classification schemes were tested:

 

 

Also the performance may have to be compared to random guess schemes.

 

Table 2 through Table 5 show the classification results. In most cases, LD and NN-2 showed best performance than the other two schemes and also than the two RG schemes.

Nearly all classifiers failed to detect the glasses, bandana, and also “funny” expression which are all characterized as extreme minority, i.e., whose prior probability is very low.

 

 

Table 2. Comparison of k-NN (), LD, NN-2 (), NN-3 (), RG-1, RG-2 for gender classification.

k-NN

detect

miss

 

LD

detect

miss

male

823

454

 

male

1,026

251

female

402

317

 

female

375

344

 

 

 

 

 

 

 

NN-2

detect

miss

 

NN-3

detect

miss

male

1,008

269

 

male

763

514

female

378

341

 

female

544

175

 

 

 

 

 

 

 

RG-1

detect

miss

 

RG-2

detect

miss

male

1,277

0

 

male

753

542

female

0

719

 

female

305

414

 

 

Table 3. Comparison Comparison of k-NN (), LD, NN-2 (), NN-3 (), RG-1, RG-2 for expression classification.

k-NN

detect

miss

 

LD

detect

miss

serious

586

511

 

serious

936

161

smiling

468

368

 

smiling

623

213

funny

0

63

 

funny

0

63

 

 

 

 

 

 

 

NN-2

detect

miss

 

NN-3

detect

miss

serious

932

165

 

serious

963

134

smiling

617

219

 

smiling

593

243

funny

0

63

 

funny

0

63

 

 

 

 

 

 

 

RG-1

detect

miss

 

RG-2

detect

miss

serious

0

1,097

 

serious

504

593

smiling

836

0

 

smiling

437

399

funny

0

63

 

funny

1

62

 

 

Table 4. Comparison of k-NN (), LD, NN-2 (), NN-3 (), RG-1, RG-2 for glasses detection.

k-NN

detect

miss

 

LD

detect

miss

on

0

8

 

on

0

8

off

1,988

0

 

off

1,986

2

 

 

 

 

 

 

 

NN-2

detect

miss

 

NN-3

detect

miss

on

2

6

 

on

0

8

off

1,962

16

 

off

1,958

30

 

 

 

 

 

 

 

RG-1

detect

miss

 

RG-2

detect

miss

on

0

8

 

on

0

8

off

1,988

0

 

off

1,988

0

 

 

Table 5. Comparison of k-NN (), LD, NN-2 (), NN-3 (), RG-1, RG-2 for bandana detection.

k-NN

detect

miss

 

LD

detect

miss

on

0

8

 

on

0

8

off

1,988

0

 

off

1,988

0

 

 

 

 

 

 

 

NN-2

detect

miss

 

NN-3

detect

miss

on

0

8

 

on

0

8

off

1,988

0

 

off

1,986

2

 

 

 

 

 

 

 

RG-1

detect

miss

 

RG-2

detect

miss

on

0

8

 

on

0

8

off

1,988

0

 

off

1,988

0

 

 

From this experiment, I concluded that

1)      Samples from minority class (with very low prior probability) tend to be miss-classified with any classifier;

2)      Eigenface approach is good for identity recognition purpose, robust to noise and partial loss of data, but not as good for classification purpose dealing with extraneous face samples, i.e., not used for the eigenface generation.

 

 

Remarks

 

After Monday presentation, I applied AdaBoost on LD and Parzen window for each classification and obtained preliminary results, but the classification performance was not improved so much. Particularly, I am looking into the working details for Parzen window since my preliminary results were far from those in [2]. Mostly due to limited time, multi-linear analysis method has not been attempted. Future direction of study should include the analytical and experimental study of multi-linear analysis method. 

 

 

References

 

[1]         Richard O. Duda, Peter E. Hart, and David G. Stork, Pattern Classification. New York, NY: John Wiley & Sons, 2001.

[2]         Tiwari, “Face recognition: eigenfaces with 99 PCA coefficients,” MAS.622J/1.126J Project Presentation, MIT, Fall 2004. [ppt]

[3]         W. S. Yambor, “Analysis of PCA-based and Fisher discriminant-based image recognition algorithms,” Master's thesis, Dept. of Comp. Sci., Colorado State Univ., July 2000. [pdf]

[4]         M. Turk and A. Pentland, “Eigenfaces for recognition,” J. Cogn. Neurosci., vol. 3, no. 1, pp. 71-86, 1991. [pdf]

[5]         H. A. Rowely, S. Baluja, and T. Kanade, “Neural network based face detection,” IEEE Trans. Pattern Anal. Machine Intell., vol. 20, no. 1, pp. 23-38, Jan. 1998. [pdf]

[6]         Face recognition homepage. [Online]. Available: http://www.face-rec.org

 

*This page has been written as a final project report for MAS.622J/1.126J. Pattern Recognition and Analysis taken in Fall 2006.