HMM of Loan Performance Data
Using the Loan Performance data, build a model (or models) that accurately detect whether a loan will default using a minimum number of observations.
Motivation
Lenders on Prosper have access to a dashboard that provides information regarding their portfolio of loans. Besides return on investment (ROI) information, lenders are able to review the current status of all open loans. Many lenders who use Prosper often complain about the slow response time of the Collection Team responsible for dealing with defaulted loans. We propose a solution that reduces the complexity of monitoring active loans.
Goals and strategy
We hoped to accurately classify whether a loan would be paid back or defaulted using as few months of loan performance observations as possible. To this end, we attempted to construct models the hidden states for which might show the hidden "financial health" of the borrower. We believed that a financially healthy state might be more likely to emit observations of "current", but lower financial healths would be more likely to emit a status of "late".
HMM Training
Data Preparation
The Prosper LoanPerformance table contains status updates for loans. The table is updated periodically, and the status changes according to whether payments have been made on time. Statuses in the database include:
| Status | Number of entries in database |
|---|---|
| Current | 387711 |
| 4+ months late | 52475 |
| 1 month late | 22071 |
| Late | 20107 |
| 2 months late | 16985 |
| 3 months late | 14736 |
| Paid | 8556 |
| Charge-off | 2929 |
| Defaulted (Delinquency) | 1523 |
| Payoff in progress | 856 |
| Defaulted (Bankruptcy) | 237 |
| Repurchased | 71 |
The loan performance table contains many entries which are odd or contradictory, including multiple entries per month, some of which indicate "late" and others which indicate "current". To simplify this, we did a majority vote of the statuses in each given month to arrive at a single status per loan per month.
HMM Structure
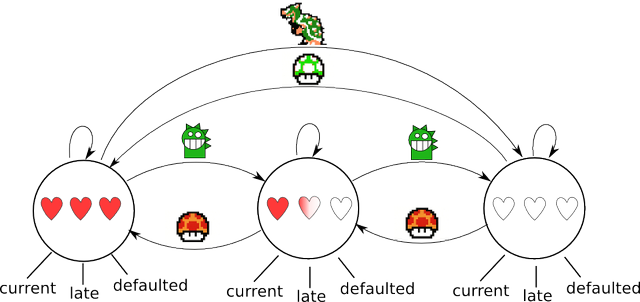
We constructed 3 HMM models, with 3 nodes, 5 nodes, and 6 nodes. In each case, we trained two versions of the model: one with all sequences ending in "Paid", and one with all sequences ending in "Defaulted". That way, we could calculate the probability that each model would produce a given test sequence, allowing us to determine with what probability that sequence would end in a default.
Here is the Source code for the HMM models, the annonymized data, and trained models.
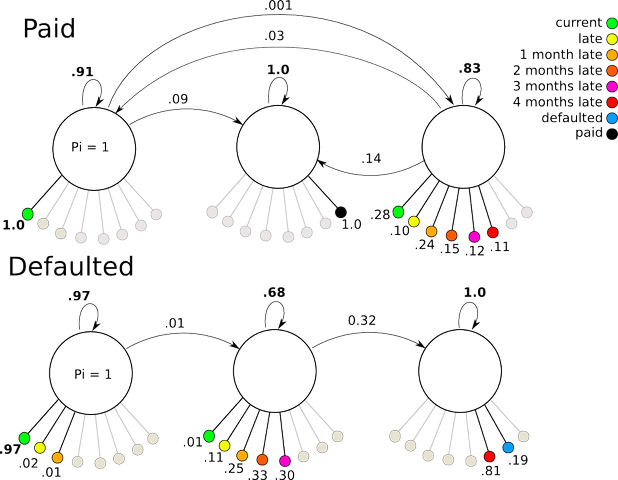
3 State HMM
The 3-state model trained with "Paid" data ended up behaving more or less as expected, with the exception that states 2 and 3 inverted. There is a high probability of remaining in state 1 and continuing to emit "current" signals. From state one, a small probability allows transitions to either state 3 (from which late and current signals can be emitted) or moving directly to state 2 where the final "paid" observation is produced. The "Defaulted" model functions similarly, but with a more direct progression from state 1 (with some chance of lateness), to state 2 (with a high chance of lateness), then state 3 for a default.
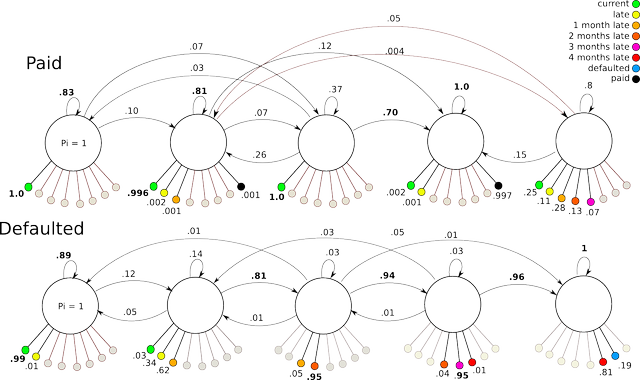
5 State HMM
The five state model performs similarly to the 3 state model for the defaulted case. For the paid case, the transitions become very complex and odd with low parsimony.
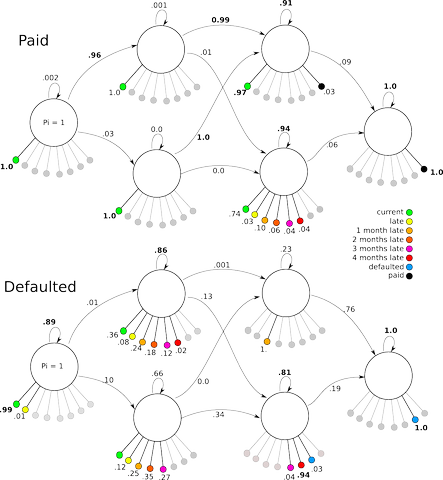
6 State HMM
The 6-state model was constructed to match a design proposed by Rabiner to allow parallel paths between two possible outcomes. The idea was to create a "healthy" path across the top side of the model, and an "unhealthy" path across the bottom side, each allowing cross-over to the other side, and culminating in the final state on the right. Whereas in the other models transitions between any node to any other were allowed, in this model, left-to-right transitions were enforced. Again, the "paid" model showed lower parsimony than the "defaulted" model.
Results
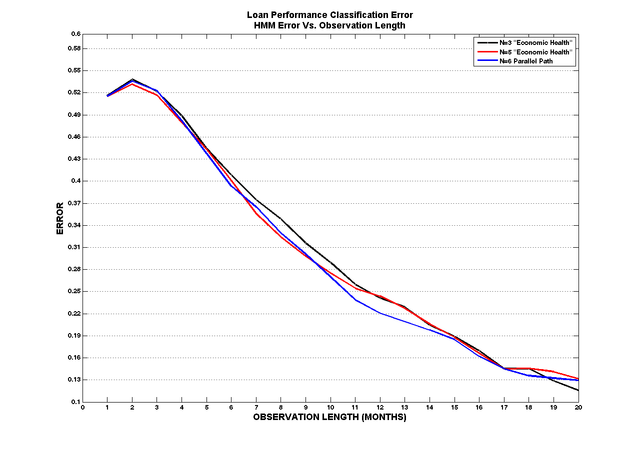
By comparing the log likelihoods of an N state HMM trained on paid performance data and an N state HMM trained on default performance data we achieved satisfactory performance. The graph below represents classification error vs. the length of an observation. Given > 4 months of observation you have greater than a 50% chance of detecting whether a loan will default. We graphed the results for all 3 models but did not explore the classification error when you mix an N state paid model with an N state default model.
Future Improvements
We achieved satisfactory performance using 2 N state HMMs and comparing the log likelihoods . In our current 2 N State design, the starting state is always state one. Perhaps this is not necessarily true, however since all loans start in a “current” state, according to our models of economic health, the logical starting place was state one. More interesting and perhaps more useful to Prosper, is to specify a single model of economic health and to train it on both the paid and defaulted observation data. Then, given an observation sequence, we could look at the posterior state probabilities to indicate how “likely” the loan might transition to a hidden state with large observation probabilities of defaulting. The idea is that the by looking at the posterior probabilities of the final observation in the sequence, Prosper could use that posterior state probability and some threshold to flag a loan in danger of defaulting. As an analytical tool, it allows Prosper to forecast how many loans are likely to default in the current month. The uses of this information are plentiful. Additionally, if the model trained up as left to right model, you could use Viterbi to decode the most probable states and see how “close” the last hidden state is to the hidden state of lowest economic health. This may not be as interesting.
Conclusion
We prototyped and characterized a model of economic health trained on Prosper’s Loan Performance data. Our goal was to use HMMs to build a classifier and by comparing the log likelihoods of the 2 HMMs, accurately flag a loan as a default. We achieved satisfactory performance, yet it is obvious that as a loan’s history increases with time, our classification error decreases. We also suggested another method using a single model trained on both sets of state to evaluate the posterior probabilities to predict if a loan is likely to default.