Material Computations
by denamolnar
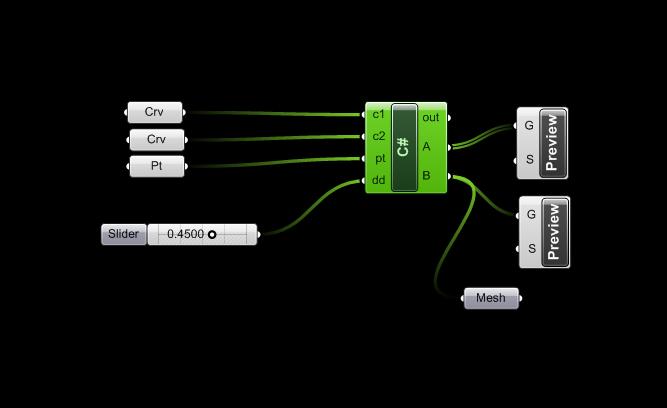
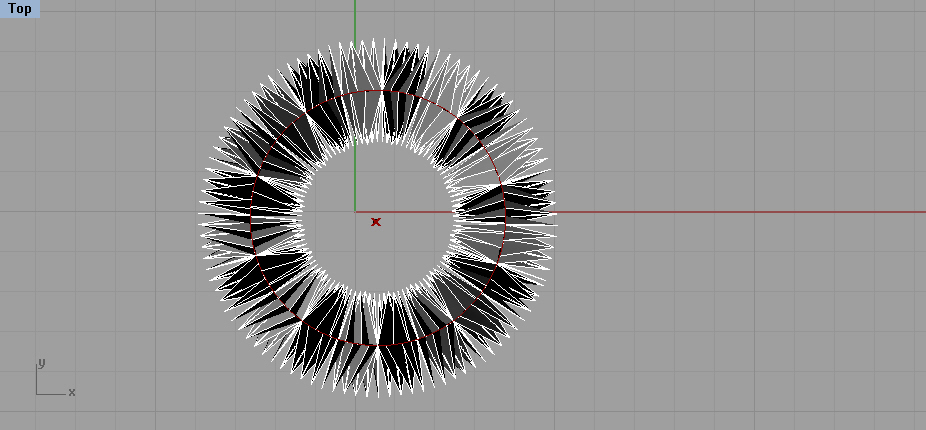
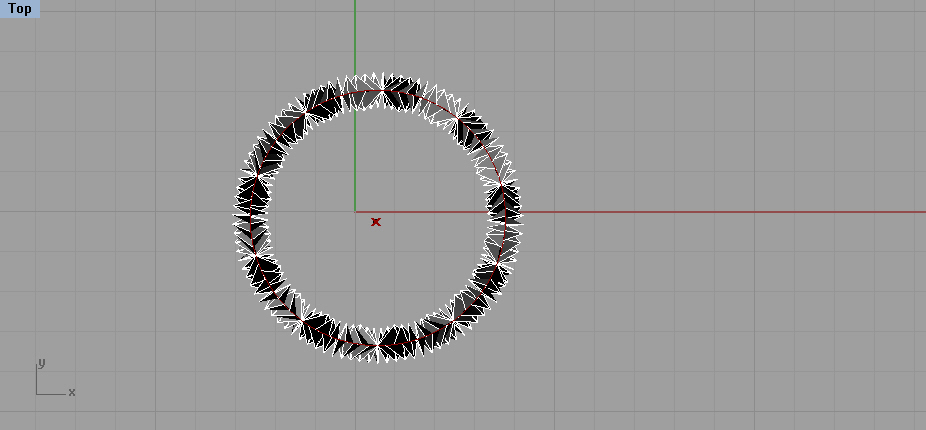
I have always been interested in patterns that were capable of change. For my Computational Design Project, I chose to design a circular pattern that could deform in shape and size. Using Grasshopper, which is a plug-in for Rhino, I used pre-determined values and a code to generate a 3 dimensional cylinder that expands and contracts at its center. I then used the top views of the cylinder’s deformed surface to capture different radial shapes for laser cutting and embroidery design.
Grasshopper plug-in with Slider to adjust radial shapes
Shapes generated by moving the slider
Below is an image of one of the shapes imported into Ilustrator as a 2 dimensional vector file for use on the laser cutter and embroidery machines. When I imported the file, many layers of lines were produced as a result of the 2d image being a projection of a 3d object. I had to delete any duplicate lines in order to prevent the laser cutter from over etching a single line, and to prevent the embroidery program from crashing. Over etching in areas did produce some nice results as well however. The darkest lines seen in the design below (creating a circle) were over etched and caused the center circle to fall away from the etched border. This allowed me to mix and match different patterned/colored circles for the center of the design.
Once imported into the laser cutting program, I used felt as the base for the design to be etched onto.
Various shapes were pieced together with a fabric adhesive
Finished laser etched designs
Embroidery
Finished embroidery
Rhino/Grasshopper C# code