Introduction
Reinforcement learning is a class of problems in machine learning which focuses on an agent searching through an environment in which the agent perceives its current state and takes actions. The algorithm seeks the environment to find the best policy for maximizing cumulative reward for the agent [1]. It differs to classes of problems that were mostly dealt within this class. Most of supervised and unsupervised learning algorithm concentrates on minimizing the classification error rate. There are no given classification error for state and action pairs while rewards are only given to the environment.
When a computer learns how to play chess, there can be two possible ways. The first way is to teach best moves for each case. It can be thought as supervised learning. Neural networks or other supervised learning solutions can be applied in this case. However, if such information is not given and you are only given a final goal of your task (winning the game by checkmate can be the final goal), the agent needs to learn by it which action to take for each possible case in the given environment. The event like checkmate (win) is called reward or reinforcement. Reinforcement and reward can be received not only at the end of a trial, but can be given at any time. The objective of reinforcement learning then is to find the best policy for each state in the environment to reach the goal.
When it takes too many steps to reach to a goal state, it usually takes too long to find the best policy that reaches the goal.
Moreover when one policy for the goal has been found, the agent may tend to use only the discovered policies and not to explore for other policies. This process is called 'exploitation'. When the agent exploit too much, there are chances that the agent fall into the local maxima.
In order to solve this problem researchers have proposed an way to facilitate an agent with an intrinsic reward.
Singh, et al. [4] proposed the figure 1 below as an example of setting a critic inside an agent.
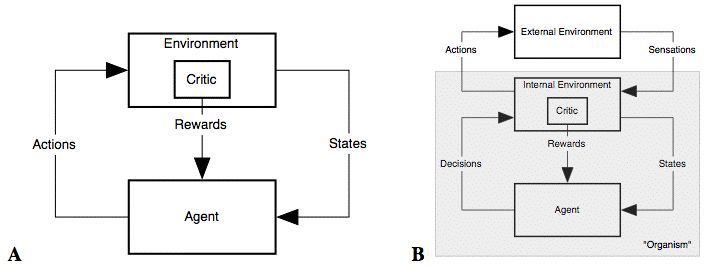
Figure 1: Agent Environment Interaction A: The usual view B: An elaboration [4].
The model has a copy of external environment called an internal environment and the actual agent interacts with the internal environment only.
In this structure, the inner critic gives the reward rather than the outer environment and salient sensory inputs to an agent also can be a reward which is not set outside the environment. Moreover, rewards can be diminished if such action is taken too many times by the agent. This makes differences to the older model in that rewards were only given from the outside the environment.
Objectives of the project
The main objective of the project was to understand various internal reward algorithms in reinforcement learning, observe agent's behavior in each algorithms, and try to find a better way to adapt this algorithm to human robot interaction.
- Understand different aspects of both internal rewards implementation
- Compare two different internal reward algorithm in various environments
- Adapt the algorithms to the interactive reinforment learning situation, the Sophie Environemnt.
Overview of Reinforcement Learning
The below is the formal definition of reinforcement learning [8].
- States : s or si, i = 1 .. N (number of states)
- Actions : a or ai, i = 1 .. M (number of actions)
- Policy : π(s) - an action at state s, π - all policies for all states. a policy of an environment.
- Utility : Uπ(s) = E[ Σ∞t=0 γR(st) | π, s0=s ]
* The Utility is supposed to measure the performance of a given policy.
* The Utillty is the expectation of future rewards from the given state s.
- Transition Probability : T(s, a, s') the probablity of transition to s' when an action a is taken at the state s.
Passive Reinforcement Learning
- Bellman Eq. : Uπ(s) = R(s) + γ Σs' T(s, π (s), s') Uπ(s')
* γ : discount factor
- Temporal Difference(TD) Eq. : Uπ(s) = Uπ(s) + α * ( R(s) + γ Uπ(s') - Uπ(s))
* No T(s,a,s') model is needed.
* α : learning rate, this is used instead of the transition probability model.
* Since the TD method does not use the probability model for the tansition, it learns slower than ADP(Bellman eq.) and show high variability.
Active Reinforcement Learning
- Bellman Eq. : U(s) = R(s) + γ maxaΣs' T(s, a, s') U(s')
- No given policy. It learns its policy through the process.
Q-Learning 's Formal Definition
In this project, Q-learing was used and below is the equation for the Q-learning.
- U(s) = maxaQ(s,a)
- Bellman eq. : Q(s,a) = R(s) + γ Σs'T(s,a,s') maxa'Q(s',a')
- TD eq. : Q(s,a) = Q(s,a) + α * ( R(s) + γ maxa'Q(s',a') - Q(s,a))
The TD Q-learing does not need a model for either learning or action selection. For this reason, Q-learing is a model-free method [8].
Intrinsically Motivated Reinforment Learning (Intra-Option Learning about Temporally Abstract Actions)
Singh, et al. [4] proposed a method called 'intrinsically motivated reinforcement learning'. It uses an intra-option learning method proposed by Sutton, et al. [5]. Option learning has its own Q-value function and a probability model for each options. At each state an agent can foresee the rewards taken by each options. As a result, an agent becomes less likely to explore aimlessly and tries to achieve sub options as quickly as possible and finally reach the goal state. The below is the suppoed algorithm by Singh.



Figure 2 : Learning Algorithm for Intrinsically Motivated Reinforcement Learning [4].
Overview of the algorithm
- Current state st, current action at, extrinsic reward ret, intrinsic reward rit are given.
- Obtain the next state st+1
- Register the option if st+1 has a salient event of the given option.
- Caculate the intrinsic reward (is on only when the st+1 is salient.
- For each option, if st+1 is in the initiation set add stA.
- For each option, update the reward and probablity model.
- Update Qb according to st, at.
- Update each Qb (st, o)
- Update Qo (st, at), Qo (st, o')
- Choose next action using e-greedy policy w.r.t. Qb
For each option it keeps,
- Initiation Set Io
- Qo Value, keeps the policy for getting to the option's final state.
- P(s|s') , probability from states to states
- Ro, option reward function
Maximizing learning progress: an internal reward system for development
Kaplan, et al. [3] proposed the progress driven reward system. The below is the equation for the progress definition.
Kaplan defines the progress as the reduction of the prediction error. As the predicition becomes more accurate the progress diminishes and the exploration stops.
- Π (SMR(t)) -> SMR(t+1)
- Π Predictor
- Πs(SMR(t-1)) -> S'(t), e(t) = distance(S'(t),S(t))
- p(t) = e(t-1) - e(t) : e(t)<e(t-1)
- p(t) = 0 : e(t)≥e(t-1)
- R(t) = {p(t)}
The reward at time t is the progress at time t.
Environments used for the test

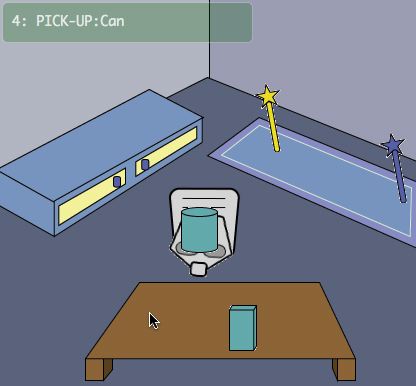
Figure 3: Sophie's Kitchen(on the left) and Sophie's Playroom(on the right) Environment used for the testing [6].
The Kitchen Environment
- The environment has five objects: the flour, the egg, the spoon, the bowl, and the tray.
- Objects can be put either on the table or the shelf.
- There are two possible states for the tray: empty or mixed.
- There are five possible states for the bowl: with egg, with flour, with egg and flour, mixed, empty.
- There are five actions available: turn left, turn right, pick up an object, put an object, use an object to an object.
- Only mixed tray can be put into the oven.
- The agent can be in three locations: heading to the shelf, heading to the table, heading to the oven.
The goal of the kitchen environment is to bake a bread. First the agent needs to mix the egg and the flour. In order to do this, the agent needs to fill in the bowl with both the egg and the flour and then stir with the spoon. The mixed bowl needs to be poured into the tray. Then tray goes into the oven and the goal is reached.
The Playroom Environment
- The environment has four objects: the box, the cylinder, the blue wand, and the yellow wand.
- Objects can be put on the table, the rug, and the chest..
- There are two possible states(colors) for the cylinder and the box: blue and red.
- There are five actions available: turn left, turn right, pick up an object, put an object, use an object to an object.
- The agent can be in three locations: heading to the table, heading to the rug, heading to the chest.
- Objects can be placed in four locations: on the table, on the rug, on the chest, at the agent.
The goal of the playroom environment is to make both the cylinder and the box smile. When the blue wand is used, either cylinder or box changes its color; the color changes blue to red and red to blue. When the yellow wand is used, both cylinder and box smiles only when the color of both objects are same.
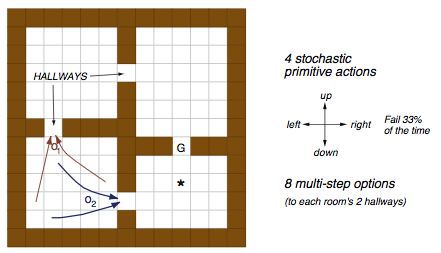
Figure 4: Maze Environment [5].
The Maze Environment
- 13x13 Maze with walls and hallways.
- The final goal is indicated as 'G' in the grid.
- There are three hall ways and two hallways are set as an option: O1, O2.
The goal is to reach the point G.
Basic Q-learning alogirhtm tested on both Playroom and Kitchen environments
Q-learning alogirhtm without any intrinsic reward were tested on both environments. The below are the results for both cases.
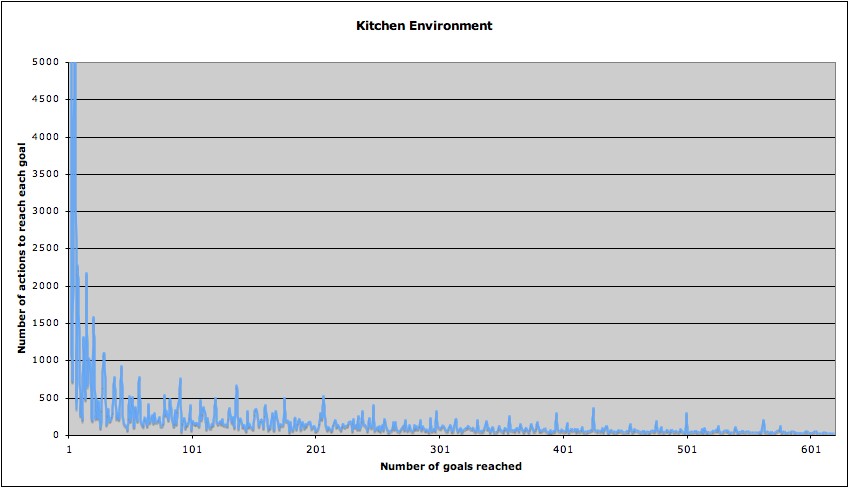
Figure 5 : RL with no intrinsic rewards in the Kitchen Environment
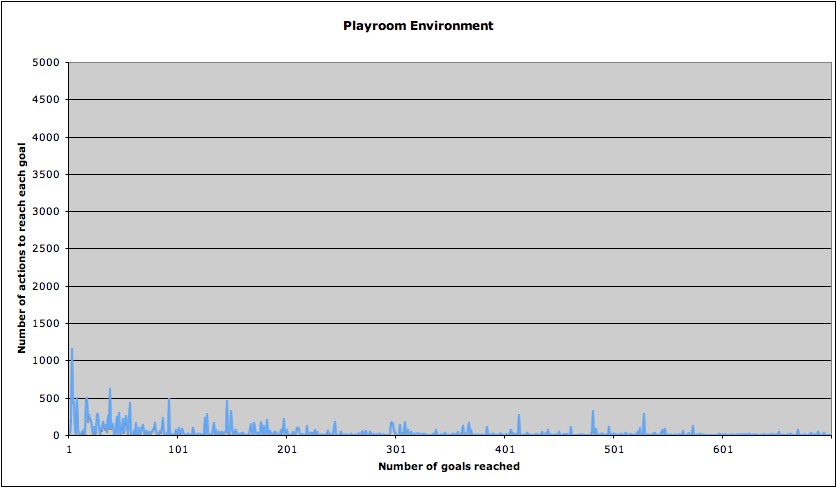
Figure 6 : RL with no intrinsic rewards in the Playroom Environment
From above graphs, it is easy to know kitchen problem is significantly harder to solve. Even though it took much less step to reach the goal first in the playroom environment, it did not took fast enough to actually converge to the optimal policy. Even between 500 and 600 trials, you can see the glitch. This seems due to the uncertainty of goals in the playroom environment. There are several different goals in the playroom environment.
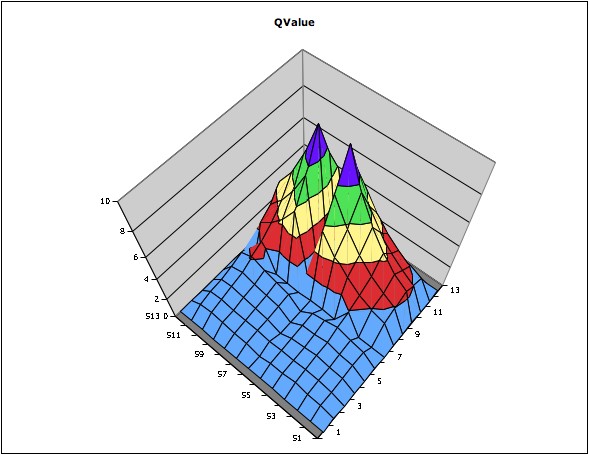
Figure 7 : Q-values plot for the maze environment
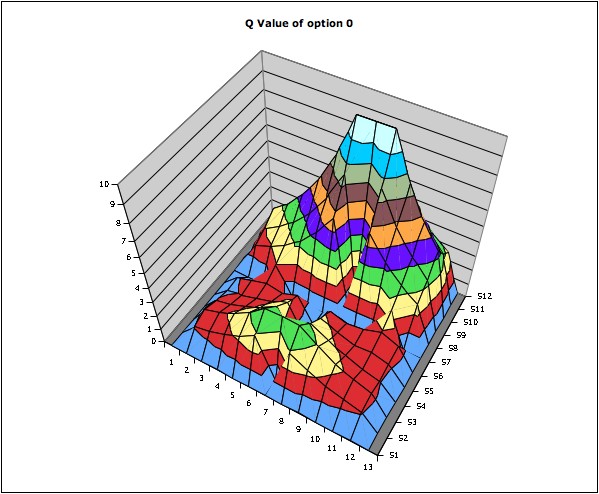
Figure 8 : Q-values plot for option 0 for the maze environment
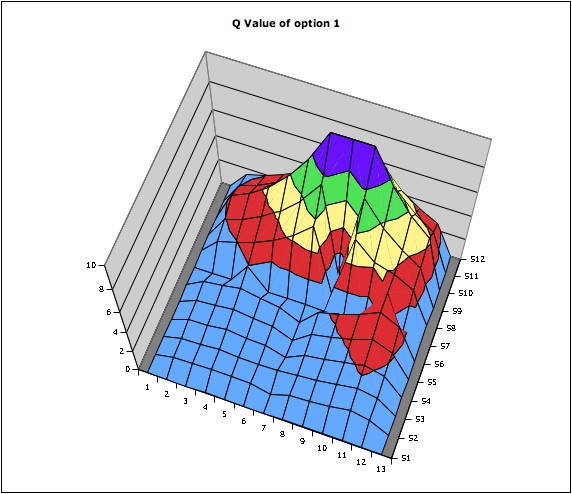
Figure 9 : Q-values plot for option 1 the maze environment
The above plots shows how each option (internal reward) affects in the q value space. The value in each position means maxaQ(s,a). From figure 8, you can see the q value of option 0 around the option 0 has been uplifted. In figure 9, the area around opt1 has been a little uplifted however it seems the q values for option 1 have not been trained enough. Because of the difficulties in choosing the right values for each constant, it was hard to find the best values for both awards for options and the final goal, learning rate, and discount rate. Therefore, the foreseeable option q value did not work well and the option policies were not selected when choosing an action with the maximum Q value; the Q(s,o) was too low.
Conclusion
Due to the difficulty of understanding the algorithms and finding right values for learning, only option learning was implemented and tested. However, I was not able to implement on the Sophie environment. Therefore I ended up finding right constant values for the Maze environment. However studies from the Maze environemnt, I could know that the nagative reward for the taking each step should be lesser than the total steps taken to reach the goal times the final reward. Also discount and learning rate is also important in that it accounts how the intrinsic and salient event rewards affects to the whole q values.
Discussions for HRI
The option learning algorithm proposed by Singh, et al. took quite long time to actually learn given options; it took a million operations. For a human to try to make an agent learn all the necessary values such as Q-values , reward values, probability models for each option, it did not seem easy to apply the algorithm to interactive reinforcement learning environment like Sophie. Careful adjustment of constant values like learning rate, balance of reward value between option and the final goal, negative reward for taking each step are also needed. Moreover, it needs further investigation on how to apply interactive rewards to both instrinsic and extrinsic rewards for both behavior Q values and option Q values. Without these adjustments, the agent is more likely to fall into local minima or too much exploitation. Especially since internal rewards acts as a sub goal, when the final goal is too far away, it sometimes keeps to remain in the sub goal area. This leads to over exploitation and slows down the whole learning. If this happens, the goal for this project cannot be accomplished. The agent will not look more intelligent and its behaviors will more likely to be less readable to humans. It will become even harder to train an agent.
References
[1] Reinforcement learning. (2006, December 15). In Wikipedia, The Free Encyclopedia. Retrieved December 15, 2006, from http://en.wikipedia.org/wiki/Reinforcement_learning
[2] Kaplan, F. & Oudeyer, P.-Y. (2006). The progress-drive hypothesis: an interpretation of early imitation. In Dautenhahn, K. and Nehaniv, C., editor, Models and mechanisms of imitation and social learning: Behavioural, social and communication dimensions, Cambridge University Press.
[3] Kaplan, F. and Oudeyer, P.-Y. (2004). Maximizing learning progress: an internal reward system for development. In Iida, F., Pfeifer, R., Steels, L., and Kuniyoshi, Y., (Eds.), Embodied Artificial Intelligence, LNAI 3139, pages 259-270. Springer-Verlag.
[4] Singh, S., Barto A. G., & Chentanez N. (2004). Intrinsically Motivated Reinforcement Learning. Advances in Neural Information Processing.
[5] Sutton, R. S., Precup, D., and Singh, S. (1999). Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence, 123, pages 181-211.
[6] Thomaz, A. L. and Breazeal, C. (2006). Reinforcement Learning with Human Teachers: Evidence of feedback and guidance with implications for learning performance. In Proceedings of the 21st National Conference on Artificial Intelligence (AAAI).
[7] Sutton, R. & Barto, A. (1998). Reinforcement learning: an introduction, Cambridge, MA, MIT Press.
[8] Russell, S. J., Norvig, P. (1995). Reinforcement Learning, chapter 21, pages 763-789. Artificial Intelligence: a Modern Approach. (2nd Ed.) Prentice-Hall.
|